【10分で電卓マスター】統計検定２級で必要な電卓の使い方を解説します

こんにちは。ハレトです。

突然ですが私ハレトは、先日統計検定２級に無事合格しました!!🎊　
勉強期間は２か月ほど頑張りました。（勉強のスケジュールは別記事にてまとめる予定）

統計検定２級では事務用電卓の使用が認められていますが、ここで質問です。

『MRC』『M+』『M-』といったキーの意味を知っていますか？

統計検定２級では、これらのキーを知っておくことで、かなりの時間短縮になるんです！

私もテスト２日前にこれを習得したおかげで、すっごく計算が楽になったのでこの記事で一緒にマスターしていきましょう。

この記事では統計検定２級で最低限必要な使い方を押さえていきます。

そもそもどうして覚える必要があるの？

統計検定２級の勉強をしていると、

\[\frac{\bar{x} – \mu}{\sqrt{\frac{\sigma^2}{n}}}\]

といった複雑な式を計算することがよくありますよね？（ちなみにこの数式は、母分散既知の母平均の信頼区間推定より）

これを計算しようとすると、分母と分子を別々に計算してメモしておき、また計算する必要があると思います。

この記事で紹介するキーを使いこなせればメモする必要はなく、一回の計算で済ませることができるんです。
便利でしょ？

電卓のキーをマスターしよう

というわけで早速、『MRC』とか『M+』といったキーの使い方を見ていきましょう！

概説

M+　→　メモリーの数に足す

M- 　→　メモリーに保存されている数から今の数をひく

MRC →　メモリーから数を呼び出す

メモリーとは計算機の脳みそみたいなもので、ここに数字を１個だけ保存できます。最初の値は0です。

この説明で分かる方は少ないと思うので、具体例と共に見ていきましょう。

M+　〈イメージはメモリに足す〉

今表示されている数字を、メモリーに足します。

メモリーとは計算機の脳みそのようなもので、数字を１つだけ覚えておくことができるものでした。そして、メモリの初期値は0です。

例

12を押したあとに『M+』を押すと、0+12=12がメモリーに保存されました。

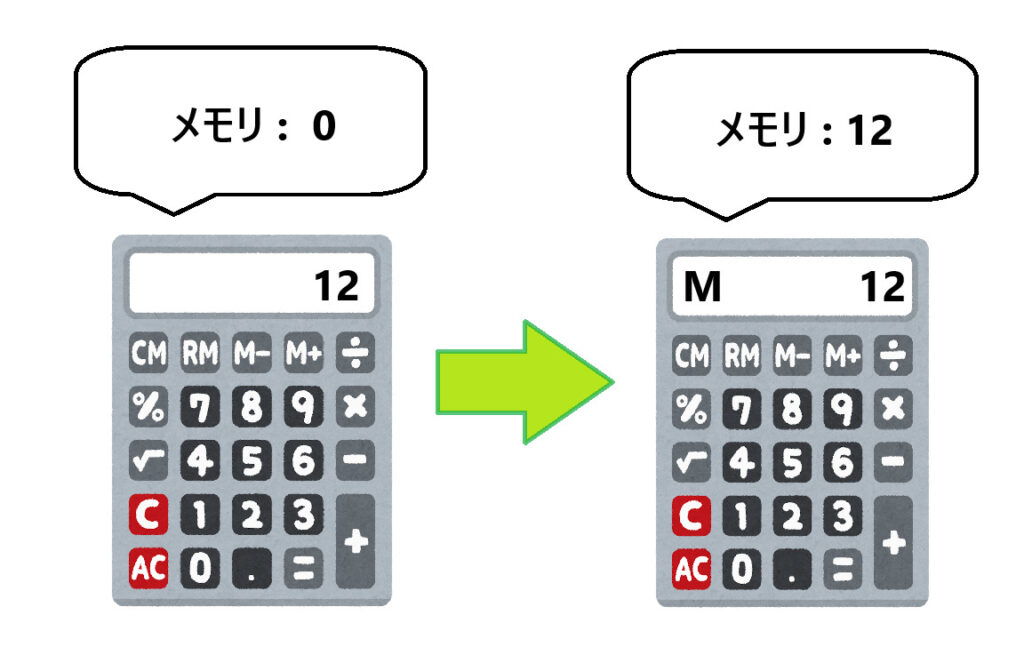
12の後に、さらに14を押して『M+』を押すと、12+14=26がメモリーに保存されます。

M- 〈イメージはメモリから引く〉

ひとことで言うと、M+の逆です。　メモリーからその数をひいてメモリーに保存します。

例

14が表示されていて『M-』を押すと、 0-14=-14がメモリーに保存されました。

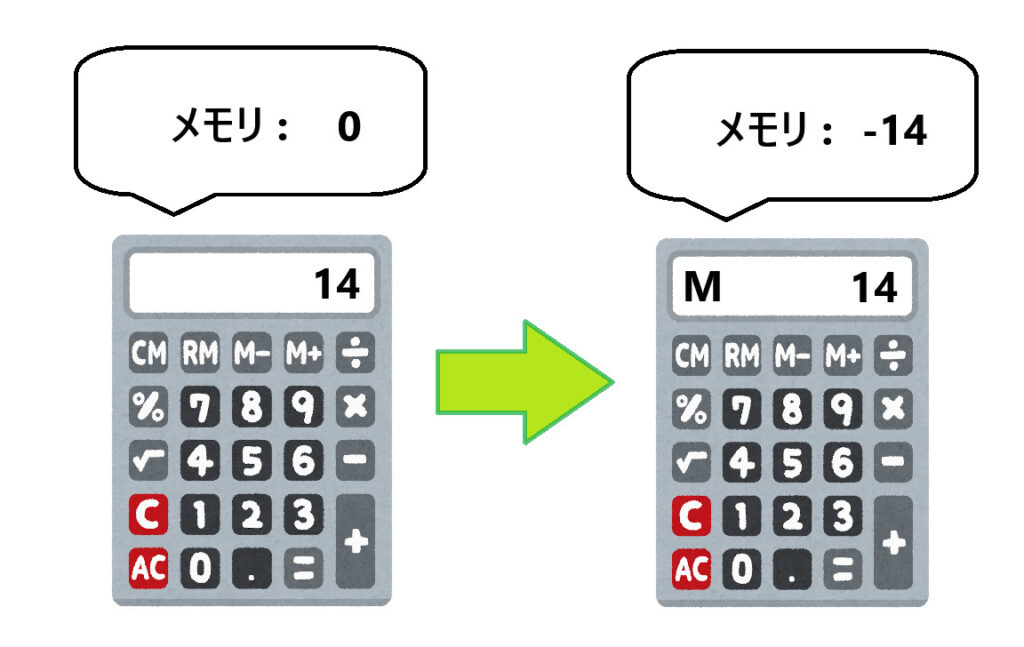
さらに15を押して『M-』を押すと、-14 – 15 = -29がメモリーに保存されます。

MRC　〈メモリーの数を呼び出す〉

先ほどまでメモリーに保存していた数を呼び出します。パソコンのペーストが近い意味ですね。

必要なタイミングで『MRC』を押すと、先ほどの数を貼り付けます。

例

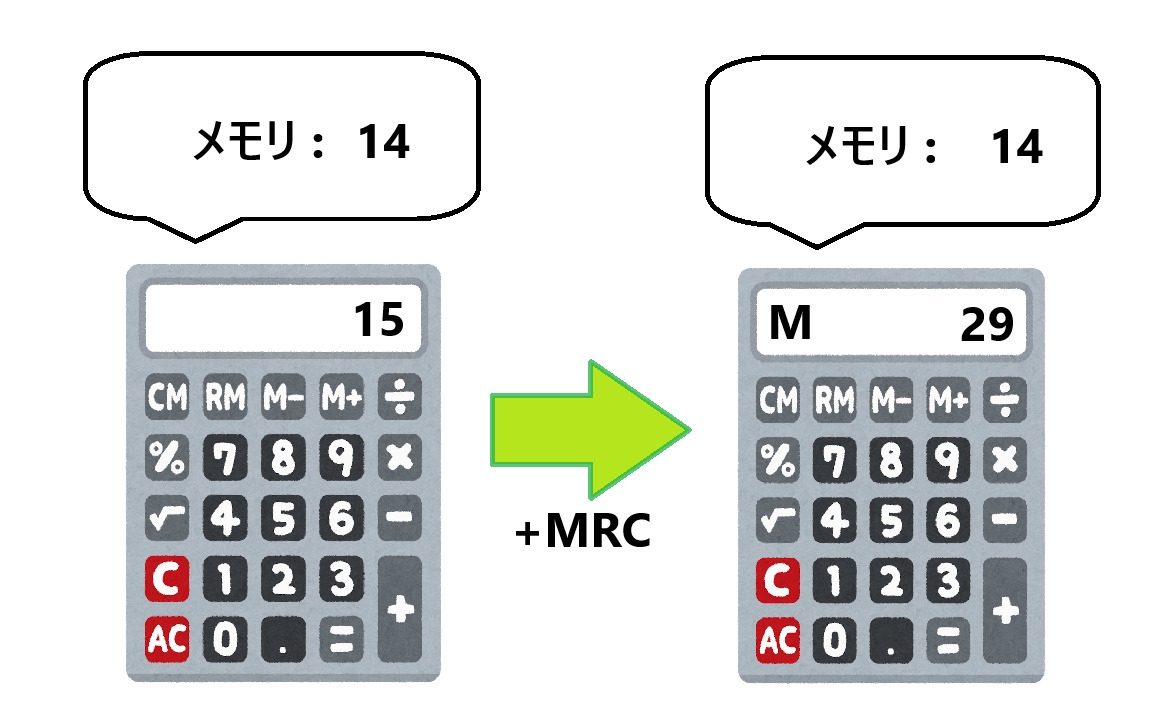
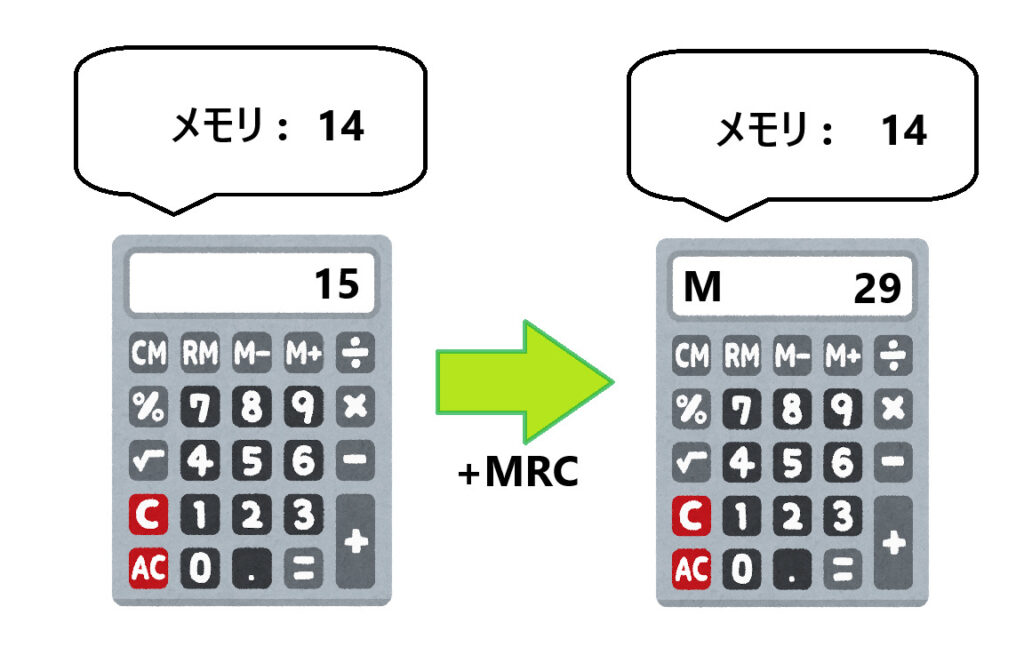
メモリーに14が保存されていて、『15+MRC』を計算すると、15+14=29になります。

練習問題

問１　(M+とMRC)

$$(2+5)×(4+3)$$

次は試験でも使いそうな式です

問２　(M+とMRC)

$$\frac{10.5-10}{\sqrt{\frac{3.3}{30}}}$$

あとがき

ここまでご覧いただきありがとうございます。

例ではM-を使う問題を用意できませんでした。というのも、試験ではM-は使用しなかったからです。おそらくM+とMRCがあれば事足りると思います(^^♪

それでは本記事はここまでです。ほかの記事もぜひご覧いただけると嬉しいです！