最近の投稿
- 【20分で電卓マスター】統計検定2級で必要な電卓の使い方を解説します
- インターンのグループワークで大学院生が無双していた件
- 【実体験】友達じゃないと言われたら考えたいこと
- 基本情報技術者試験の科目bを5日で対策した話
- 狭山湖の謎の建物の正体とは?実際に行って調べてみた

 ハレト
ハレト増減表も矢印の意味も訳分かんないよ!

大丈夫だ!この記事を読めば一発でできるようになるぞ!
増減表はグラフを書くときに必要になる表です!
グラフと言っても、3次以上の関数をグラフにするときに必要になります。

二次関数は平方完成して、頂点の座標を求めてグラフを書いてきたと思います。
三次以上の関数でも同じように、山や谷になってるところの頂点
つまり、極大値(一番山になってるところ)と極小値(一番引っ込んでるところ)を求めることで、グラフが書けるようになるんです。
それに加えて↘↗を書き加えたりした増減表を書くことで、より正確なグラフを書くことができます。
とにかく増減表はめっちゃ重要
〇次関数とは、一番次数が大きいものを見ます
(例) $$f(x)=3x+1⇛1次関数$$
$$f(x)=5+4x^6+3x^5+4x^3⇛6次関数$$
$$f(x)=x^4+3x^2+3⇛4次関数$$
極小値と極大値をまとめて極値と言います。
 ハレト
ハレトどうやって極大値と極小値の座標を求めるの?
まず極大値も極小値どちらも、接線を引いてあげると、‥

どちらも傾きが0になっています。
つまりこれらから次の関係がわかります。
極値をとる点での接線の傾き=0
要するに、接線の傾きが0になるような座標を探せば良いということです。
 ハレト
ハレト『関数を微分した値が接線の傾き』だったよね?
 先生
先生そうじゃ。要するに f'(x)=0 を解けばよいということなの。
 先生
先生ちなみにf'(x)はf(x)を微分した値という意味だよ。
①で極値を求めましたが、傾きが0になる座標がわかっただけで、それが極小値なのか極大値なのかまだ分かりません。
そこで、極値の周りの接線の傾きに注目して、極小値か極大値かを判別していきます!
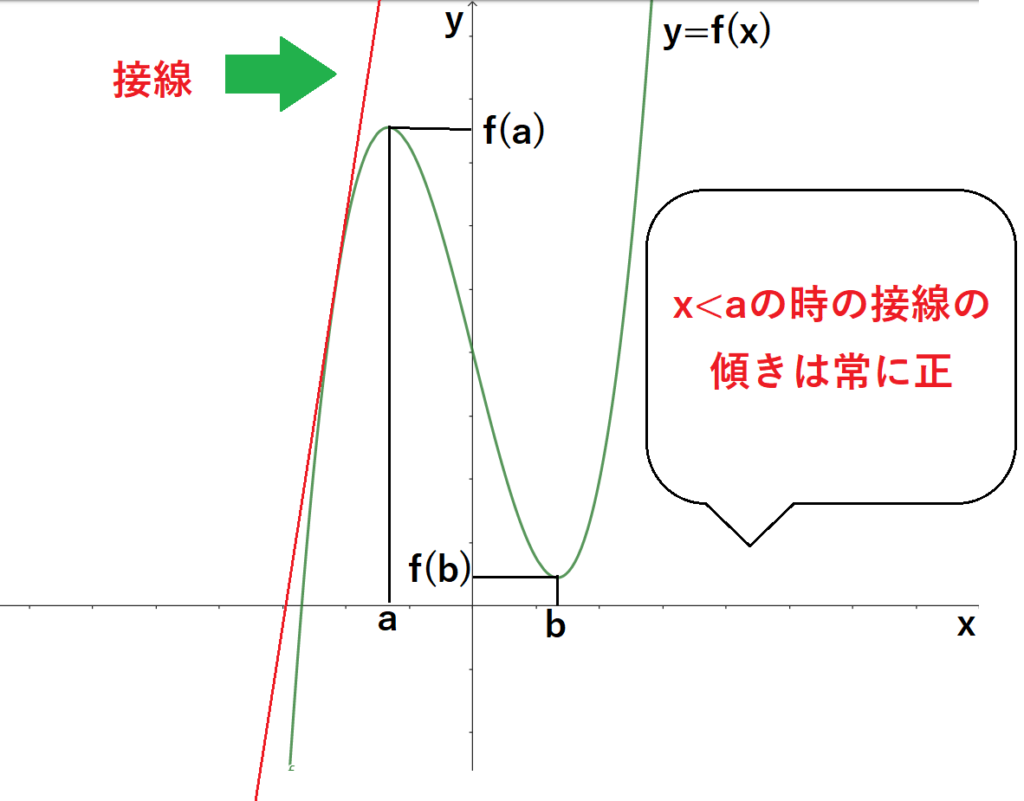
下のグラフでは、x座標がaより小さいときは、接線の傾きはいつも正になっていますね!
つまり、f'(x)>0ならグラフは右肩上がりになるわけです。(重要)
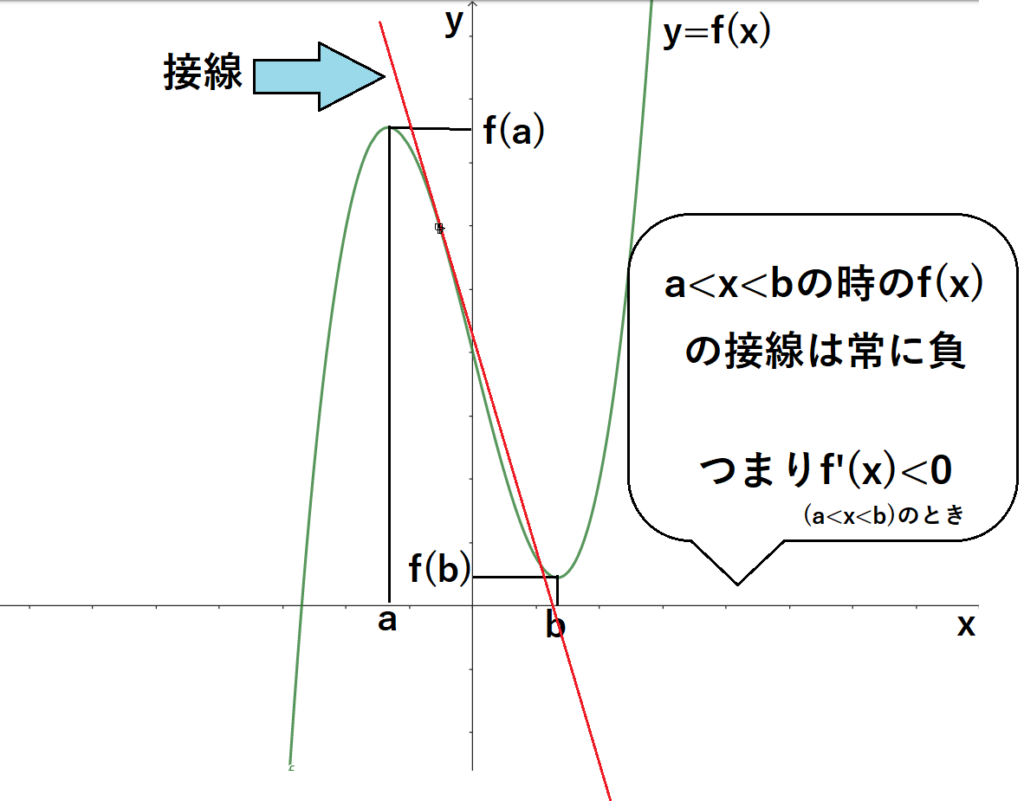
a<x<bのとき接線の傾きは常に負になっています。
つまり、f'(x)が負になれば、グラフも右肩下がりになるわけです。(重要)
ラストはb>xのときです。
b>xの時はどこでも接線の傾きは正になっています。
つまり、f'(x)>0ならば、グラフは右肩上がりになっているんです。(重要)

以上のことをまとめると‥‥
・f'(x)>0ならグラフは右肩上がり
・f'(x)<0ならグラフは右肩下がり
これで原理は網羅しました!
次は具体的に増減表を書いてみましょう!
増減表はこのように書きます。
プラスマイナスや↗↘の位置は関数によってもちろん違います。

では手順にそって書き方を紹介します!
ここからy=f(x)について考えます!
まずは、x,f'(x),f(x) で3行の表を作ります
こんな感じです

f'(x)はy’と書かれることもあり、f(x)はyと書かれることもあります。
極値のx座標(傾きが0になるところ)を見つるため、f'(x)=0を解きます。
すると、xの値がいくつか出ると思います。
そのxが極値の候補なのですべて一行目にひだりから小さい順に書きます。
今回はx=a,b(a<b)がf'(x)=0の解とすると‥

と書けます。
それ以外のマスにもつながっていることを示すために、…を書いておきます。
関数にy=f(x) (-4<x<8) など、定義域が書かれているときは両端の値も書きます。
例えば(-4<x<8)なら、両端に-4と8を加える..
次に手順2で埋めたxの値の下を計算して書き入れます。
f'(a)とf'(b)は傾きですが、極値での接線の傾きなので明らかに0になります。
f(a)とf(b)は関数f(x)にそれぞれの x の値を代入して求めましょう。

こうなりますね♪
…の下を埋めていきます。
前章の原理で解説した通り、極値と極値の間は傾きは変わりません。
このことを踏まえて、…のところにある数を自分でテキトーにもってきて代入して考えます。
f'(x)の段には、代入した結果が正なら+
代入して負ならーを書き入れます。
f(x)の行のところには、
上のますが+なら↗を
上のますがーなら↘を書き入れます。
注意
下の図は、問題によって、プラスマイナスが変わります。矢印の向きも問題によって変わるので注意です♪

これで増減表は完成です!
さっきの増減表をもとにグラフを書くとこんな感じ(もちろん問題によってグラフは変わります。)
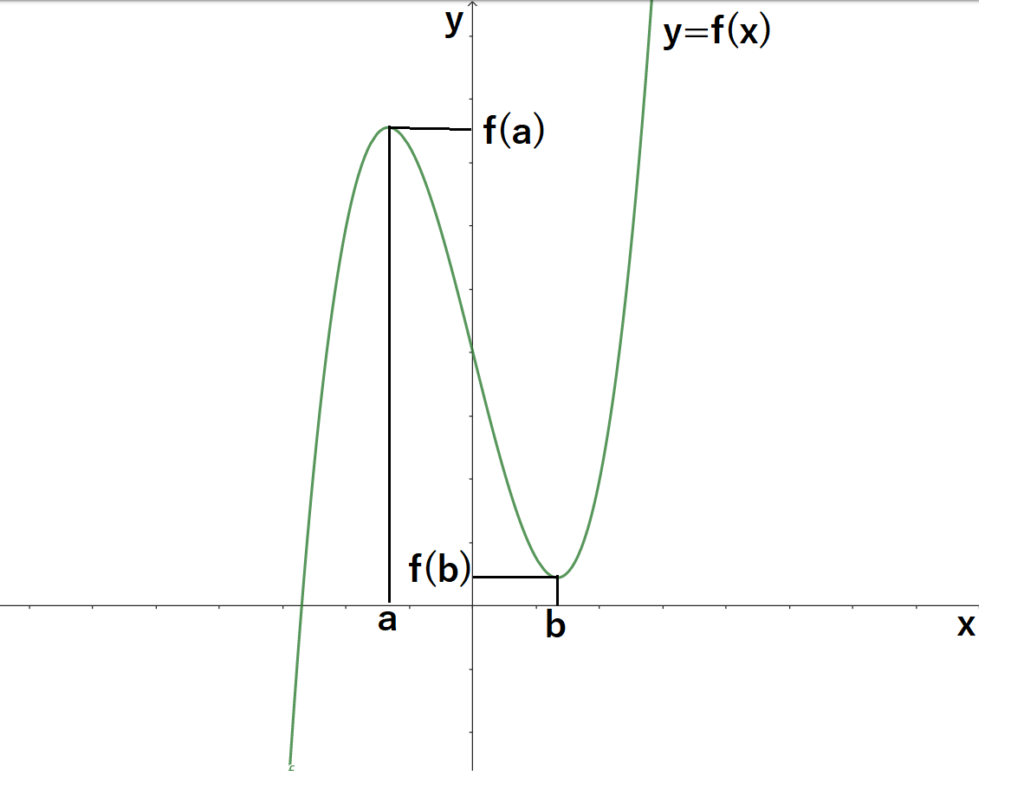
 ハレト
ハレトなるほど…。なんとなくわかったけど。文字がおおいね。
 先生
先生具体例を見ていくとよくわかるぞい!
ここからは、具体的な数で増減表を書いていきましょう!
$$f(x)=x^3-3x^2-9x+11$$の増減表をかけ。またグラフもかけ。
①まず極値を求める
極値はf'(x)=0となる所だったから、これを解くと、
$$f'(x)=3x^2-6x-9=0\ \ \ x=-1,3$$
よって増減表を少し埋めてみると、このようになります↓
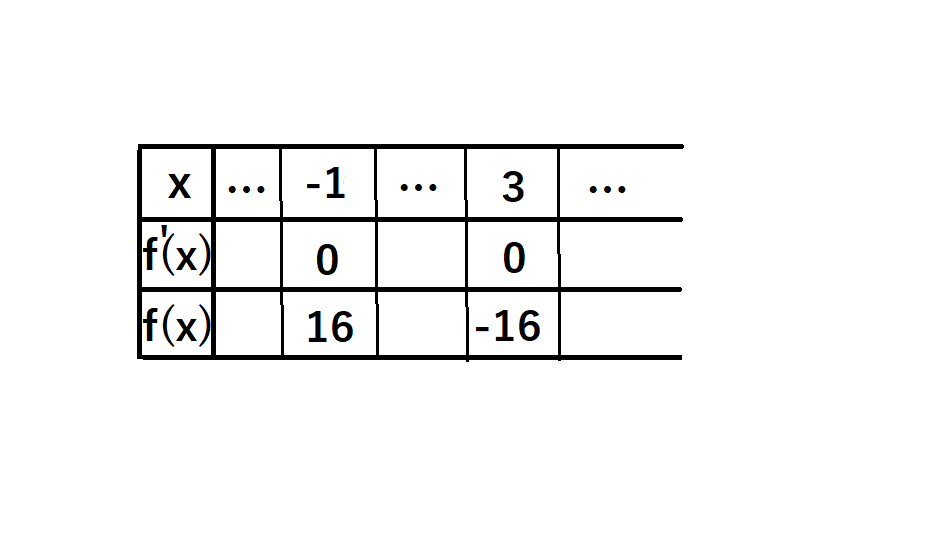
②次に、二行目のあいているところに+-を書き入れます。
書き方は、適当なxの値を持ってきて代入すればよかったから、
x<-1のところでは、x=-2を(もちろんx=-10でもそれ以上小さくてもOK)
-1<x<3のところでは、x=0を(もちろん2でも1でもOK)
3<xのところでは、x=4で考えると、(もちろんx=20でもなんでもOK)
f’(-2)>0 ⇛よってx<-1のところではつねに増加しているから+を書く
f’(0)<0 ⇛よって-1<x<3のところでは常に減少しているから-を書く
f’(4)>0 ⇛よって3<xのところでは常に増加しているから+を書く

これで増減表は完成!
この表を見ながらグラフを書いてみましょう!
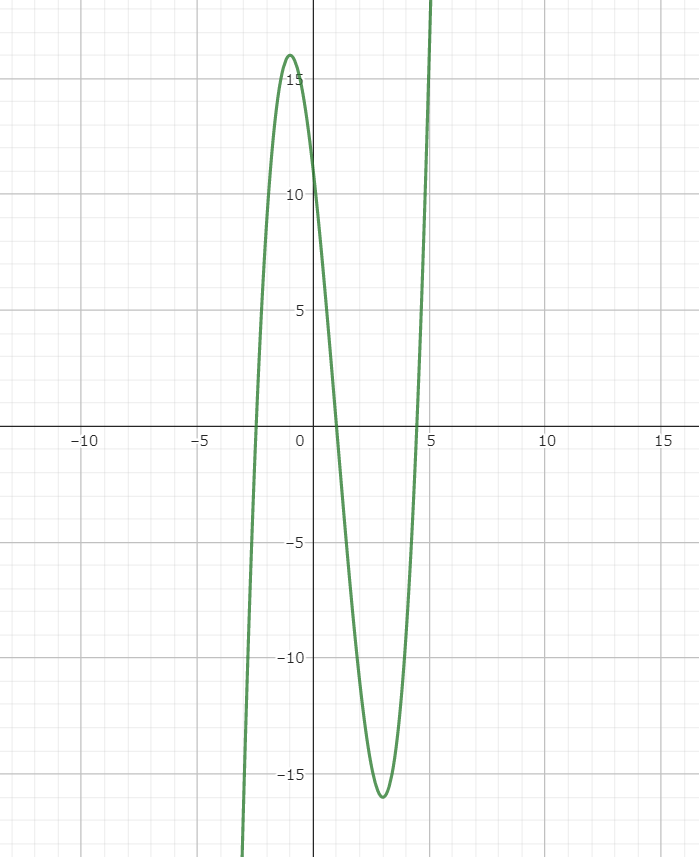
こうなります。
極大値と極小値の座標さえ取れてれば、問題ないです♪
もう一問
$$f(x)=-\frac{1}{3}x^3-2x$$の増減を調べ、極値があればその極値を求めよ。グラフもかけ。ただし、実数の範囲内で考えること。
まずは極値の座標を求めましょう。
$$f'(x)=0を解くと、x^2=-2$$
これは実数の範囲内では解けないので、極値はありません。
つまり、山にも谷にもなる所がないということです
想像がつかない人は必要ないですが増減表を書いてみましょう!
こんな感じで描けます。
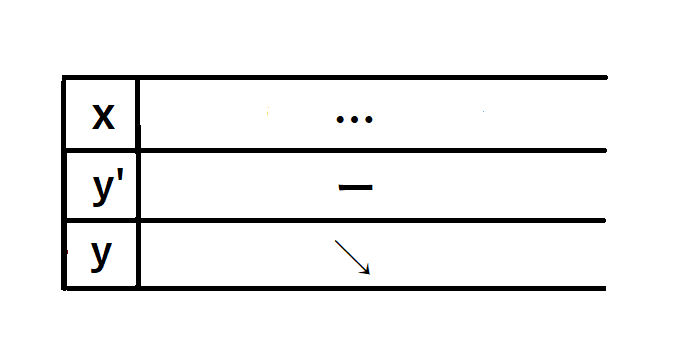
よって、『極値はなく、単調減少する』が答えです。
 ハレト
ハレト極値がないこともあるんだね
次の関数の増減表を書いて、極値を求めよ。$$f(x)=-2x^3+3x^2+12x$$
解答⇛ x=2で極大値20,x=4で極小値-32をとる
まずは極値を求めます。
f'(x)=0を解くと、
x=2,-1となるからこれをもとに増減表を書くと、

これで増減表は完成。
極値は、 x=2で極大値20,x=4で極小値-32をとる
増減表を書くには、
①f'(x)=0をとく
②3行の表を書いて、①のxの値を左から小さい順に記入する
③二行目には、f'(x)>0なら+をf'(x)<0ならーを記入する
④三行目に、上のマスが+なら↗を、ーなら↘を記入する
です!
この流れは覚えてしまいましょう。
ほかの記事もぜひご覧ください(^_-)-☆
コメント