最近の投稿
- 【統計検定準１級】分散共分散行列が半正定値であることを証明します
- 統計検定２級はノー勉で合格できるのか計算してみた
- 統計検定2級の試験当日の持ち物を紹介します
- 【10分で電卓マスター】統計検定２級で必要な電卓の使い方を解説します
- インターンのグループワークで大学院生が無双していた件
統計検定２級はノー勉で合格できるのか計算してみた
この記事は、統計検定２級の勉強途中に考えたことを、それはもうざっくりテキトーに計算してみる回です。
ツッコミどころがあれば、記事最後のコメント欄にお手柔らかにご指摘いただけると嬉しいです♪
それではスタート！
もくじ
統計検定２級の合格点60点のハードルは高い？低い？
試験勉強を進めていた時に、ふと『テスト60％ってノー勉で受けても合格できるかもしれない？』と思いました。
普通に考えたら、5択ですし35問程度あるので満点とるなら\(\frac{1}{5^{35}}\)の確率ですからね。まあ無理なんですが、、
さんそ君ちょ、ちょ待てよ
ビリヤードのタマ話終わっちゃったタマ…
とはいえ、60%以上得点すれば合格できますので、今回はその確率を計算していこうと思います！
ノー勉で受かるのはどのくらいの確率？
二項分布と正規分布近似の２パターンで求めていきたいと思います。
仮定すること
・受験者は、統計の知識ゼロ＆試験はランダムに選ぶ.
・選択肢は5つで全35問.
・配点は均等.
ハレトこの仮定は簡単のために設定します
①二項分布で受かる確率を計算してみる
5択問題を35問解く。この時当たる総数が従う分布は何だったでしょうか？
ビリヤードのタマ二項分布タマ
その通り！二項分布で考えてみましょう。
イケメソ1号二項分布を知らなくても、確率の求め方は理解できると思います。
確率変数Xが二項分布に従うとします。つまり、
$$X\approx B(35,\frac{1}{5})$$と書けて、確率質量関数は、
\[ P(X = k) = {\scriptsize{35}}{\large{C}}{\scriptsize{k}} \cdot (\frac{1}{5})^k \cdot (1-\frac{1}{5})^{n-k} \]です。
合格点は６割以上でしたので、35(問)×0.6=21(問)以上正解すればよく、この確率を求めると
\[ \sum_{k=21}^{35} P(X = k) = \sum_{k=21}^{35}{\scriptsize{35}}{\large{C}}{\scriptsize{k}} \cdot (\frac{1}{5})^k \cdot (1-\frac{1}{5})^{n-k} \]この計算は、、、無理です。
ビリヤードのタマ頑張ってくれタマ(´;ω;｀)
というわけで、pythonさんに計算してもらうと～
from scipy.stats import binom
n = 35
p = 1/5
prob = sum(binom.pmf(k, n, p) for k in range(21, 36))
print(prob)
2.5350516297520324e-07 ≒ 0.0000002535 ≒ 0.00002535 %
という結果になりました。
完全ランダムネスに選択すると、この確率で合格することが出来るようですね♪
ビリヤードのタマ無理に決まってるタマ( ;∀;)
②ド・モアブルの定理を使って求めてみる【おまけ】
統計の分野ではおなじみのド・モアブルの定理でも、受かる確率を求めてみたいと思います。
①と同じことを求めるので、気になる方以外は飛ばしてもらってOKです。
ド・モアブルの定理
二項分布\(Bin(n,p)\)はnが十分大きいとき、正規分布\(N(np,np(1-p))\)に近づく。
つまり、 確率変数\(X\approx Bin(n,p)\)のとき、nが十分大なら\( \frac{X-np}{\sqrt{np(1-p)}}\approx N(0,1) \)
つまり、 確率変数\(X\approx Bin(n,p)\)のとき、nが十分大なら\( \frac{X-np}{\sqrt{np(1-p)}}\approx N(0,1) \)
（\(\approx\)は分布に従うの意）
合格点は６割以上でしたので、35(問)×0.6=21(問)以上正解すればよく、この確率を求めると
$$P(X \ge 21) \simeq P(X \ge 20.5)=P(\frac{X-7}{\sqrt{7\cdot\frac{4}{5}}} \ge \frac{20.5-7}{\sqrt{7\cdot\frac{4}{5}}}) $$
$$ここで、\frac{20.5-7}{\sqrt{7\cdot\frac{4}{5}}} \simeq 5.705$$
よって、最右辺は標準正規分布に従うから、正規分布表を参照すると、
ほぼ0ですね。私の表にはこの数値は小さすぎて載っていませんでした。
【追加検証】何回受験すれば合格できるのか？
合格する確率は、2.5350516297520324e-07 ≒ 0.0000002535 ≒ 0.00002535 % でした。
確率がかなり低く、「これじゃ受からないじゃん！」と思われた方に提案です。
受かるまで受験してみよう
というわけで、ここからは後半パート。試験に受かるためには、何回くらい試験を受ければ良いのか、これを計算で求めていこうと思います。
【実践】何回受験すれば良いか計算してみる
求めるための方針
確率なので100%受かるという断言はできないので、高確率で受かる受験回数を求めていきます。
求め方は、１回でも受かれば良いので余事象で求めていきましょう。つまり、
（合格する確率）＝１ー（n回受験して１度も合格しない確率）
を計算していきます。
実際に計算する
計算が煩雑なので、python で計算します。
まずは、90%の確率で合格する受験回数を求めます。
受かる確率をpとおきます。
n回受験して合格する確率が0.9以上になる最小のnを求めたいので、
$$1-(1-p)^n \geq 0.9$$ $$0.1 \geq (1-p)^n$$両辺自然対数をとると、
$$n \cdot \log(1 – p) \leq \log(0.1)$$ \(log(1-p)\)が負であるので、両辺これで割ると不等式が逆転して、 $$n \geq \frac{\log(0.1)}{\log(1 – p)}$$最後の不等式をpythonで計算します。
import math
p = 2.5350516297520324e-07
n = math.ceil(math.log(0.1) / math.log(1 - p))
print(n)結果：9082990（回）でした。
ビリヤードのタマこんなに受験したのに、まだ90％タマか…。
math.ceilの使い方はこちらのサイトで解説されています。
合格する確率と受験回数とお金
というわけで同様にほかの確率も求めた結果の一覧はこんな感じ！
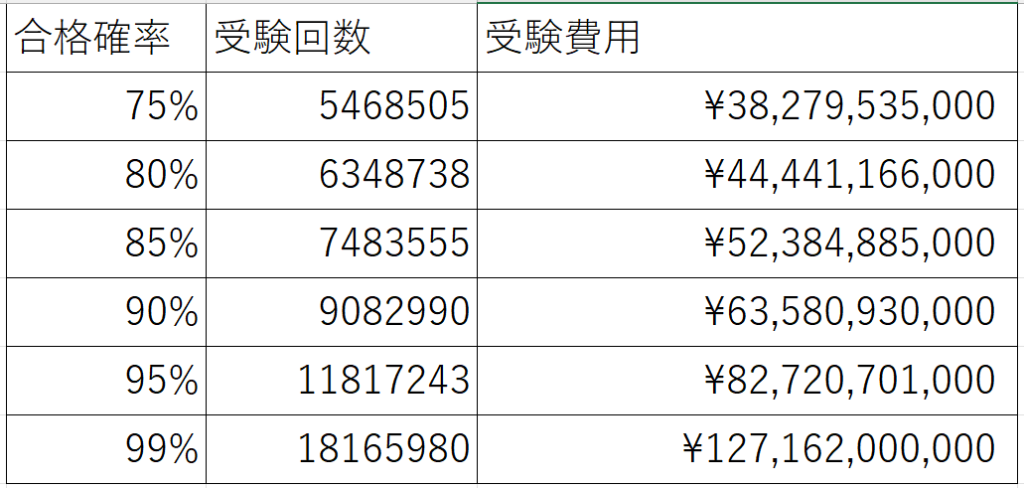
お金の単位が読みづらいと思うので、以下に書きなおしました。
| 合格確率 | 受験回数（回） | 受験費用（円） |
| 75% | 5468505 | 382億7953万5千 |
| 80% | 6348738 | 444億4116万6千 |
| 85% | 7483555 | 523億8488万5千 |
| 90% | 9082990 | 635億8093万 |
| 95% | 11817243 | 827億2070万千 |
| 99% | 18165980 | 約1271億6200万 |
ビリヤードのタマあ、あ…、こんなお金ないタマ…。
【結論】ノー勉で受かろうとすると、たぶん財産が底をつくほうが早い
合格する確率は（ほぼ）０％でしたし、合格するまで受験し続けたとしても、おそらくお財布がすっからかんになるのが先でしょう。
というわけで、まぐれ合格を狙うのは無謀だということが判明しました。
ただし、今回は選択肢を完全ランダムに選ぶことが出来るなど、かなり条件を簡約にしている背景もあるので、必ずしもこの結果が正しいとは言い切れません。
例えば、似たような選択肢があると排除する。といった何かしらの攻略法があれば、受かる確率も上がりますからね。
とはいえ、受験費用もばかにならないので、着実に勉強したほうがコスパがよさそうですね。
というわけで今回はここまでです。最後までご覧いただきありがとうございました！
コメント